浮点数详解

发表于 更新于 分类于 阅读次数： 本文字数： 1.3k 阅读时长 ≈ 5 分钟

根据通用国际标准IEEE754,详解单精度浮点数. 除特殊标注外,下文中的浮点数专指单精度浮点数.

浮点数表示方法

32位浮点数存储格式:1bit符号+8bit指数为+23bit尾数.

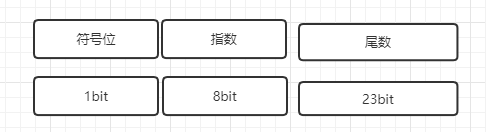
  1. 使用S表示符号位
  2. 使用e表示指数位, 为了节省空间我们使用无符号整数来, 那负数如何表示呢? 将e+127的结果存储在指数中. 我们将其称为阶数, 用E表示,则有:\(e=E-127\) . 其中E>1且E所有位不全为1,也不全为0.
  3. 使用m表示尾数位, 并且规定, 尾数必须是 \(1 \le m \le 2\)​ , 可以去掉尾数固定的1, 使用M表示尾数中小数部分.

可以得到浮点数的计算公式:\((-1)^{s}*1.M*2^{E-127} \quad (E>0 且E的所有位非全1)\)​

规格化浮点数

规格化浮点数: 指数位非全0,非全1.

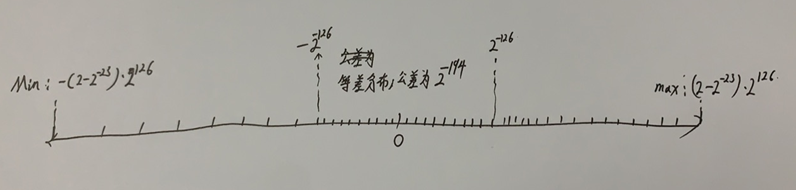
最小的正规格化浮点数为\(1.0*2^{1-127} = 2^{-126}\), 最大的负规格化浮点数为\(-1.0*2^{1-127} = -2^{-126}\). 并且将所有能表示的数字按照从小到大排列后, 发现该数列在远离0点的方向,数字之间的间距越来越大. 最小间距为\(2^{-149}\), 最大间距为最大与次大之间的差, 即\((2-2^{-23})*2^{127}-(2-2^{-23}*2)*2^{127} = 2^{-23}*2^{127} = 2^{104}\).

规格化浮点数范围为:\([-(2-2^{-23})*2^{127}, -2^{-126}] \cup [2^{-126}, (2-2^{-23})*2^{127}]\), 且将能表示的数按照从大到小排列后, 两段数列, 距离0点越近, 差越小, 精度越高.

非规格化浮点数

阶码全部为0即为非规格化浮点数. 非规格化浮点数用于表示0以及靠近0的数.

  • 规格化浮点数:按照 且的所有位非全\((-1)^{s}*1.M*2^{E-127} \quad (E>0 且E的所有位非全1)\)方式存储的浮点数.
  • 非规格化浮点数: 阶码为0的浮点数为非规格化浮点数, 即\(E=0\) . IEEE745规定, 非规格化浮点数的指数偏移值比规约数指数偏移值小1, 即126. 所以非规约浮点数的指数部分一定是\(2^{-126}\)​​.

$非规格化浮点数 = (-1)^{s}* 0.M*2^{-126} $​

次小的尾数为000...1,即\(2^{-23}\),则次小的非规格化浮点数为\(2^{-23}*2^{-126} = 2^{-149}\), 最大的非规格化浮点数为\((1-2^{-23})*2^{-126}\),并且如果将所有非规格化浮点数从小到大排列, 会构成等差数列, 并且公差为\(2^{-149}\)​.

非规格化浮点数范围为:\([-(1-2^{-23})*2^{-126}, (1-2^{-23})*2^{-126}]\), 我们再次查看规格化的浮点数范围:\([-(2-2^{-23})*2^{127}, -2^{-126}] \cup [2^{-126}, (2-2^{-23})*2^{127}]\), 并且发现\((1-2^{-23})*2^{-126}\) 与\(2^{-126}\)的差值刚好是\(2^{-149}\), 恰好是非规格化浮点数的公差. 这样可已将规格化浮点数和非规格化浮点数合并为\([-(2-2^{-23})*2^{127}, (2-2^{-23})*2^{127}]\)​ .

总结: 规格化和非规格化合并后的范围为: \([-(2-2^{-23})*2^{127}, (2-2^{-23})*2^{127}]\),并且将所有能表示的数按照从小到大排列后, 其中\([-2^{-126}, 2^{-126}]\) 的区间是等差数列, 公差为\(2^{-149}\), 除此之外, 越向两端, 间隔越大, 且最大为\(2^{104}\)​(最大与次大之间的差).

特殊数

指数位全部为1就是特殊数. 如果尾数位全部为0, 根据符号位正负,表示为正无穷或者负无穷. 尾数位非全0, 则表示NaN, not any number(除以0等操作).

总结

所以对于浮点数有以下特点:

  1. 最小浮点数为\(-(2-2^{-23})*2^{127}\),最大浮点数为:\(-(2-2^{-23})*2^{127}\).
  2. 将所有浮点数按照从大到小依次排列, 越靠近中心(0点),两个相邻数字之间差的绝对值越小, 最小为\(2^{-149}\)
  3. \([2^{-126},2^{126}]\)之间是等差分布的, 且公差为\(2^{-149}\).

所以浮点数越靠近零点,精度越高, 并且特殊说明一下在1附近的浮点数精度为:\(2^{-23} = 1.19209289*10^{-7}\)​

$ \[\begin{array} [b] {|c|c|c|c|c|} \hline 阶数(指数) & 尾数 & 表示 & 公式 &范围 & 精度\\ \hline 非全0,非全1 & 任意 & 规格化浮点数 & (-1)^{s}*1.M*2^{E-127} & [-(2-2^{-23})*2^{127}, -2^{-126}] \cup [2^{-126}, (2-2^{-23})*2^{127}] & 向两端逐渐降低\\ \hline 全0 & 任意 & 非规格化浮点数 &(-1)^{s}* 0.M*2^{-126} & [-(1-2^{-23})*2^{-126}, (1-2^{-23})*2^{-126}] & 2^{-149}\\ \hline 全1 & 全0 & \pm \infty & 无 & 无 & 无\\ \hline 全1 & 非全0 & NaN(NotAnyNumber) & 无 & 无 & 无\\ \hline \end{array}\]

\ $

参考

  1. https://zh.wikipedia.org/wiki/IEEE_754#%E8%A7%84%E7%BA%A6%E5%BD%A2%E5%BC%8F%E7%9A%84%E6%B5%AE%E7%82%B9%E6%95%B0
  2. https://chai2010.cn/static-public/talks/ieee754.pdf
  3. IEEE754规范: 四, 非规格数, ±infinity, NaN